Functors en teoría de categorías
Cómo usar Functors para separar la lógica de dominio de la representación

En el artículo anterior comentábamos que un Functor era un Mappeable — una estructura que permitía mapearse sobre si misma —, y es cierto que es así en la práctica, pero en aras de entender correctamente los conceptos que lo rigen, debemos de ponernos un poco abstractos.
Hoy profundizaremos en la idea de los Functors y después volveremos al planeta tierra para investigar posibles casos de uso.
Teoría de categorías
En matemáticas un Functor es un map entre categorías. Entendiendo por categoría, cualquier conjunto de objetos y relaciones, y cuando hablo de objetos no me refiero a objetos de Javascript sino a cualquier tipo de elemento. Por ejemplo, un plátano pertenece a la categoría de las frutas por tener una parte dulce que protege a las semillas y podemos transformarlo en plátano frito si lo echamos en una sartén, sin que este deje de pertenecer a la categoría de frutas. Es decir, un plátano es un objeto dentro de una categoría que puede ser transformado.
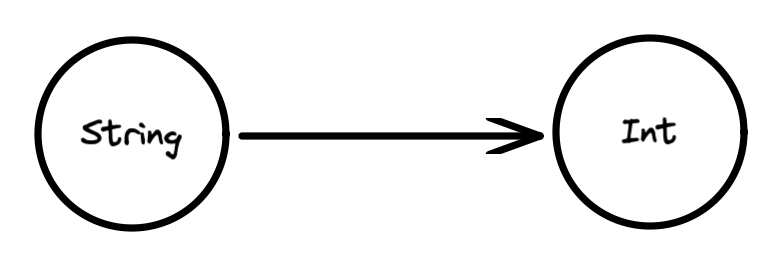
Así mismo, un número entero o una cadena de caracteres son objetos de la categoría de “tipos de datos primitivos” y se les pueden aplicar transformaciones. Estas transformaciones son llamadas morfismos y suelen estar representadas por una flecha entre dos objetos:
En este caso tenemos un String y mediante un morfismo convertirlo en un entero:
const length = str => str.length;
length("hello") // 5Nuestro morfismo es una función length que toma una cadena y devuelve un número.
Que no nos asuste el nombre de morfismo, es lo la nomenclatura que se usa para hablar de transformaciones. Al final una función pura aplica una transformación a un valor.
Lo importante aquí es que, aunque hemos transformado un String a un número entero, estos no han dejado de pertenecer a la categoría de tipos de datos primitivos.
¿Qué ocurre ahora si pensamos por ejemplo en un Array? Son los Arrays y los Strings elementos de la misma categoría? La respuesta es no, porque a diferencia de los números o cadenas de caracteres, no podemos acceder a los elementos de un Array directamente, puesto que representan el conjunto de forma interna.
Por tanto, los Arrays pertenecen a la categoría de “tipos de datos no primitivos”.
Veamoslo con un ejemplo: Imaginemos que tenemos la función double que funciona bien en la categoría de “tipos de datos primitivos”:
const double = x => x * 2;
double(2) // 4Pero qué ocurre si quiero utilizar mi función double en una categoría distinta? Por ejemplo, en la categoría a la que pertenece un Array o una Promise?
double([1]) // ups
double(Promise.resolve(1)) // upsY eso es porque double es una función (o morfismo) que solo funciona en una categoría determinada, es decir en la de “tipos de datos primitivos”.
Podríamos no obstante crear una función doubleArray y enseñarle manualmente a doblar un Array? Podríamos si:
const doubleArray = arr => {
return [double(arr[0])];
}Pero ya habíamos resuelto el cómo duplicar un número, ¿por qué tengo que redefinir el concepto de duplicar números cuando estos están dentro de un Array?
Morfismos entre categorías
Antes hemos utilizado flechas para representar funciones y hemos dicho que estas funciones son los morfismos de un objeto determinado a otro — puede ser el mismo — en una categoría dada. Si pudiéramos representar el cómo estos morfismos se aplican sobre objetos en distintas categorías podríamos hacer algo así:
Cada categoría con sus elementos y aplicando transformaciones entre ellos. La función f en ambas podrían ser nuestras funciones double y doubleArray, ambas programadas para trabajar en una categoría específica.
Sin embargo, si miramos las dos funciones vemos cierta similitud, y es que el problema de dominio de duplicar un número se resuelve de la misma forma en la categoría A y en la B. Sería genial que pudiéramos aplicar morfismos entre categorías de tal forma que solo tuviésemos una función double y fuese agnóstica a la categoría, sobre todo si mañana decidimos duplicar números dentro de promesas — no me veo creando un doublePromise —.
En el diagrama anterior hemos trazado dos flechas que “elevan” los objetos de la categoría A a los objetos de la categoría B, permitiendo el morfismo entre ellos. Sería como enseñar a nuestra función double — que solo sabe de números — a trabajar con Arrays de números, pero sin tener que rehacer la función ni crear otra.
He puesto el verbo “elevar” entre comillas porque la nomenclatura es así. Elevamos una función — lift a function — a otra categoría.
Otras veces lo he explicado cómo si fuéramos el conserje de una oficina. Como conserje de una planta determinada sabemos cómo configurar la temperatura del aire acondicionado — ya sabes que los sistemas de aire acondicionado de las oficinas solo tienen dos posiciones: núcleo terrestre o frio glacial — de la planta en la que estemos, pero no sabemos como hacerlo en otras plantas. Quizá tienen otro sistema, o quizá el cuadro de manos es distinto. No lo vemos, pues no sabemos usarlo.
Sin embargo, si tomamos el ascensor y subimos a la planta de arriba, vemos el cuadro y automáticamente sabemos cómo configurarlo — lamentablemente tiene también dos posiciones —.
Esto es lo que piensa nuestra función double cuando la elevamos de categoría. Estando en B todo le parece sencillo, ya sabe duplicar números en Arrays y puede mirar por encima del hombro a esos perdedores de la categoría A. Siempre hubo clases.
Bien, a las flechas que representan los morfismos entre categoría les he puesto la letra F en mayúscula. F de Functor, porque:
Un Functor es un mapeo entre categorías
Y si, en la práctica es un objeto con una función map, como el que tiene el Array, por eso:
[1,2].map(double) // [2,4]Map eleva a double a la categoría de los Arrays, le enseña brevemente como puede trabajar sobre números en una colección. La función hace su trabajo y se vuelve a su categoría.
Es importante notar que un Functor siempre aplica morfismos en una misma categoría, es decir lo que hacemos es subir una función de una categoría a la otra, pero la transformación se aplica sobre esta última categoría. Ósea, si hago un double sobre un Array, lo que obtengo es otro Array. Y esto es porque los Functors han de cumplir unas reglas.
Leyes de los Functors
Para que un Functor sea tratado como tal se deben de cumplir un sería de reglas, definidas en la teoría de categorías y complementadas con detalles de implementación. Las listo a continuación:
Un Functor debe de ser una estructura de datos.
Un Functor debe de permitir mapearse sobre sí mismo.
La operación map debe de respetar identidad:
Siendo f un functor, entonces:f.map(x => x) === f.
Vamos que el map debe de devolver el mismo tipo del Functor.La operación map debe de soportar composición de funciones:
Siendo fc un functor y f y g funciones de otra categoría, entonces:f.map(f).map(g) === f.map(x => f(g(x))).
La idea principal es maximizar la reutilización no teniendo que redefinir funciones de una categoría en otra, por eso es importante respetar las reglas de composición de funciones y de mantener el tipo del functor. El que después la función de transformar se llame map o then — como en las promesas — es independiente. Aunque si es cierto, que lo estándar es llamarlo “map”.
Centrarse en el problema de dominio
Cuando se nos plantea un problema a resolver tenemos que ser muy cuidadosos a la hora de no mezclar dominios. Duplicar un número es un problema de un dominio, enseñar a esa misma función a duplicar números en un array, es un problema de otro.
Una vez que resolvamos un problema para un tipo, nos debería de dar igual dónde está contenido ese tipo, ya sea un array, una promesa o un maybe. No queremos solucionar el mismo problema para cada tipo de contenedor.
Esto es lo que más problema encuentro a la hora de solucionar con enfoques tradicionales de programación orientada a objetos. La famosa encapsulación se vuelve contraproducente cuando tenemos que resolver el mismo problema para tipos distintos. En cambio, con enfoques de composición y programación funcional, las nuevas funciones son una composición de otras y la representación siempre está separada de la transformación.
Por ejemplo, se nos plantea el problema de querer representar un punto de dos dimensiones. Podríamos hacer esto:
function Point2D(x, y) {
}Digamos que ahora queremos definir el producto por un escalar, de tal forma que dado un número N, nos devuelva un nuevo punto con sus coordenadas multiplicadas por dicho escalar. Podríamos hacer:
function Point2D(x, y) {
return {
scalarProd(n) {
return Point2D([x * n, y * n]);
}
}
}En principio todo correcto. Hemos solucionado el problema. Sin embargo, la solución está muy acoplada al Point2D. La multiplicación de N números por un escalar es siempre la misma, lo que cambia es la forma en la que representamos esos números.
Si en el futuro nos surge la necesidad de tener que aplicar el producto escalar que hemos definido a por ejemplo un Array de dos números cualesquiera que no representan un punto, nos veremos en un aprieto.
Podríamos transformar esos dos números a un Point2D son para usar ese producto escalar, pero sería bastante raro:
const speeds = [10, 20];
const point = Point2D(speeds[0], speeds[1]).scalarProd(4);
const newSpeeds = [point[0], point[1]];Un array de velocidades no representa un punto — podrían ser un vector si estuvieran correlacionadas, pero no es el caso —. El código funciona, pero ¿a qué precio? Pervertimos nuestros modelos y acabamos con un programa difícil de entender.
Podríamos usar otras técnicas de composición como Functional Mixins para solucionar el problema, pero implicaría cambiar el código de la función scalarProd ya que ahora mismo es un closure y se empaqueta con su lexical scope, por lo que no podríamos extraerla para reutilizarla.
Necesitamos una solución que separe lógica de negocio de la representación. Vamos a pensar de forma aislada en una función que resuelva el problema de multiplicar por un escalar en la categoría de tipos primitivos:
const prod = a => b => a * b;Simple, fácil y reutilizable. Tenemos una función prod que toma primero un número a y después un número b. Devuelve la multiplicación de ambos.
Vamos a subirla de categoría ahora para poder operar sobre nuestro array de velocidades:
const speeds = [10, 20];
const newSpeeds = speeds.map(prod(4));
console.log(newSpeeds) // [40, 80]Funciona.
¿Qué ocurre ahora con nuestro Point2D? ¿Cómo podríamos aplicar la función prod sobre él? La respuesta es sencilla: convirtiéndolo en un Functor que permita elevar una función cualquier a su categoría:
function Point2D(x, y) {
return {
map(f) {
const [sx, sy] = [x, y].map(f);
return Point2D(sx, sy);
}
}
}Y ahora podemos usar nuestra función prod:
const point = Point2D(2, 1);
const newPoint = point.map(prod(2));Para poder visualizar el contenido de Point2D y ya que no estamos almacenando las coordenadas en ningún sitio, podemos agregar una función toString:
function Point2D(x, y) {
return {
map(f) {
const [sx, sy] = [x, y].map(f);
return Point2D(sx, sy);
},
toString() {
return `Point2D(${x}, ${y})`;
}
}
}Y ya si podemos hacer:
console.log(newPoint.toString()) // Point2D(4, 2) Y si, podréis argumentarme que este ejemplo me lo he sacado de la chistera y todo lo que queráis, pero estas cosas pasan a diario. Se hace un diseño un día, mañana aparece un caso de uso nuevo — lo normal, porque el software es algo vivo — y a darle patadas hasta que funcione y si estoy representando un Usuario dentro de un Elefante para usar su función toString, pues viva la vida.
Control sobre aplicación de funciones
Como estamos separando la representación de la función, primero ganamos en reutilización. Nuestra función prod puede funcionar en cualquier categoría que trabaje con números. Si mañana necesitamos aplicar la función prod a una Promesa, solo tenemos que elevarla a esa categoría, no programar una función prod que solo funcione con promesas.
Además, ganamos control al ser nosotros los que decidimos cuándo y cómo aplicar una función. Este es el principio en el que se basan utilidades como un Maybe.
Por ejemplo, en nuestro caso del Point2D hemos decidido agrupar las coordenadas en un array y después aplicar la función a cada uno de sus elementos por separado, pero podríamos haber seguido otro enfoque que dé más control a las funciones:
function Point2D(x, y) {
return {
map(f) {
return Point2D(f([x, y]));
},
}
}En este caso obligamos a que la función reciba una tupla de elementos y que devuelva a sí mismo una tupla de elementos. Sin embargo, ya no podríamos usar tal cual nuestra función prod, pero sí que podríamos usar composición de funciones para crear un candidato válido:
const prodTuple = n => R.map(prod(n));Estoy usando ramda para ayudarme de sus utilidades. Ahora hemos creado una nueva función prod que opera sobre tuplas sin modificar la original ni redefinir la multiplicación entre dos números. Entonces, podemos usarla en nuestro point:
const point = Point2D(2, 2);
const newPoint = point.map(prodTuple(2));
console.log(newPoint.toStirng()) // Point2D(4, 4)Conclusión
Como podéis ver el concepto detrás de un Functor es muy potente, pero tenemos que cambiar la forma de pensar: En lugar de tener objetos inteligentes que encapsulan lógica y guardan estado, y por tanto se acoplan a la representación, tenemos funciones pequeñas y puras que realizan la lógica de forma agnóstica a como se representan. Sumar una lista de números debería de ser igual, ya sea si tenemos la lista directamente o esta está dentro de una promesa.
Día a día me encuentro código qué resuelve los mismos problemas una y otra vez y esto ocurre porque las funciones, primero no son puras (usas información del exterior) y segundo están acopladas a la forma en la que se representan.
Obvio que no estoy diciendo que tiremos a la basura el enfoque de encapsulación de objetos, pero las técnicas tienen que sumar, no restar. Si el resolver un problema para un modelo de dominio en concreto, nos imposibilita el poder reutilizar esa solución sobre nuevos modelos, nos estamos tirando piedras contra nuestro propio tejado.
El enfoque funcional va de definir funciones pequeñas y puras, que compongamos entre ellas para crear nuevas funciones y si la representación cambia, llevarla de la mano hacía esa categoría y enseñarle cómo operar. Este enfoque no es mutuamente excluyendo con el orientado a objetos, podemos unir ambos paradigmas y obtener lo bueno de dos mundos.
Nada más por hoy :).